|
Автор: dist (83.102.161.---) Дата: 16-09-04 18:51 Попробуем поставить точку в вопросе с Луной, освещаемой Солнцем (см. начало здесь.) Понятно, что Луна и Солнце лежат в плоскости эклиптики (практически, ошибка не более 5 градусов), поэтому и лучи Солнца, освещающие Луну, лежат в этой же плоскости. Значит, как мы видим на небе дугу эклиптики, так будет освещаться и Луна. Если эта дуга направлена перпендикулярно к горизонту, то она будет выглядеть как прямая линия на всем протяжении, и никакого смещения выпуклости лунного серпа относительно Солнца, разумеется, не будет. Это значит, что в тропиках и на экваторе, где полюс эклиптики находится над головой, эффект смещения практически не будет заметен. Но совсем другое в наших широтах. Наклон эклиптики составит 23 градуса плюс (90 - 55) = 45 за счет широты наблюдения, что равно примерно 68 градусам, и дуга эклиптики будет наблюдаться как дуга наклонной окружности, то есть в виде эллипса. На картах неба, представляющих круговую развертку, небесный экватор выглядит как прямая горизонтальная линия, а линия эклиптики выглядит как синусоида:  В вечернее время Луна в первой четверти находится еще на восходящей части синусоиды, поэтому наклонена влево, а Солнце, находясь на нисходящей части синуосиды, вообще успевает уйти за горизонт, поэтому выпуклость лунного серпа направлена совсем не на Солнце, если смотреть по прямой. Это подверждают и рисунки планетных орбит, наблюдаемые на небе (планеты находятся в той же плоскости):   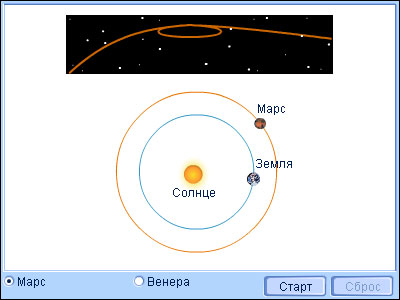 Так что странные реплики Чудака (перспектива, Солнце далеко, 5-ый класс) - не по существу. К сожалению, не работает пока вложение рисунков через ЗКА, поэтому не могу предоставить картинки, иллюстрирующие эффект с максимальной наглядностью. Следствия. 1. Прямые в пространстве практически никогда прямыми не выглядят (например, на фотографиях). 2. Любая БЕСКОНЕЧНАЯ прямая (кроме находящихся в параллельной наблюдателю плоскостии) выглядит как отрезок. 3. Соответственно, никакое равномерное прямолинейное движение таковым не выглядит (угловые расстояния меняются неравномерно). 4. В частности, это означает, что собственные движения звезд происходят по дугам и неравномерно, что обязательно должно учитываться при датировках по собственным движениям. Если кто-то найдет ссылки по обсуждаемому вопросу, буду безмерно признателен. Мне пока это сделать не удалось. Более того, астрономы (и Чудак) продожают меня уверять, что все двигается равномерно и по прямой.
|



